| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- DevOps
- MLOps
- Lv 2
- 인공지능
- mysql
- docker
- 정처기
- 프로그래머스
- 리눅스
- 데이터베이스
- 자바
- ubuntu
- Kubernetes
- github
- Ai
- db
- 자료구조
- 코딩테스트
- 쿠버네티스
- Linux
- Python
- Java
- LV 0
- programmers
- 파이썬
- git
- 머신러닝
- 코테
- 우분투
- 알고리즘
- Today
- Total
Myo-Kyeong Tech Blog
[프로그래머스] Lv.2 멀리 뛰기 (Python / Java) 본문
코딩테스트 연습 - 멀리 뛰기 | 프로그래머스 스쿨 (programmers.co.kr)
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때, 효진이는
(1칸, 1칸, 1칸, 1칸)
(1칸, 2칸, 1칸)
(1칸, 1칸, 2칸)
(2칸, 1칸, 1칸)
(2칸, 2칸)
의 5가지 방법으로 맨 끝 칸에 도달할 수 있습니다. 멀리뛰기에 사용될 칸의 수 n이 주어질 때, 효진이가 끝에 도달하는 방법이 몇 가지인지 알아내, 여기에 1234567를 나눈 나머지를 리턴하는 함수, solution을 완성하세요. 예를 들어 4가 입력된다면, 5를 return하면 됩니다.
제한 사항
n은 1 이상, 2000 이하인 정수입니다.
입출력 예
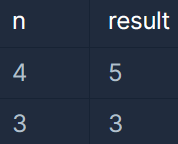
문제 풀이
"효진이는 한 번에 1칸, 또는 2칸을 뛸 수 있습니다" 라는 조건을 보고 n번째 칸에 도달하는 방법의 수는 (n-1)번째 칸에 도달하는 방법의 수와 (n-2)번째 칸에 도달하는 방법의 수를 합친 것이라고 생각하였다. 왜냐하면 효진이가 n번째 칸에 도달하기 위해서는 반드시 (n-1)번째 칸이나 (n-2)번째 칸을 밟아야 하기 때문이다.
좀 더 쉽게 예를 들면, 효진이가 4번째 칸에 도달하려면 3번째 칸에서 1칸을 뛰어야 하거나, 또는 2번째 칸에서 2칸 뛰어야 한다.따라서 4번째 칸에 도달하는 모든 경우의 수는 3번째 칸에 도달하는 모든 경우의 수 + 2번쨰 칸에 도달하는 모든 경우의 수로 계산할 수 있다.
즉, 효진이가 n번째 칸에 도달하는 모든 방법의 수는 n-1번째 칸에 도달하는 모든 방법의 수와 n-2 번째 칸에 도달하는 모든 방법의 수를 합한 것이다.
ways[n] = ways[n-1] + ways[n-2]
따라서 다음과 같은 알고리즘을 통해 문제를 풀었다.
- 1번째 칸은 1가지 방법, 2번째 칸에 2가지 방법의 수로 초기화한다. (1번째는 (1칸), 2번째는 (1칸, 1칸), (2칸) 2가지 방법)
- 3번째 칸부터 n번째 칸까지 각 칸에 도달하는 방법의 수를 계산한다. 이는 앞의 두 칸에 도달하는 방법의 수의 합이며, 계산할 때마다 1234567로 나눈 나머지를 저장한다.
- 마지막으로 n번째 칸에 도달하는 방법의 수를 반환한다.
[Python]
def solution(n):
answer = [0] * (n+1)
answer[1] = 1
answer[2] = 2
for i in range(3, n+1):
answer[i] = (answer[i-1] + answer[i-2]) % 1234567
return answer[n]

위의 풀이로 문제를 풀었더니 테스트1에 런타임 에러가 발생했다..ㅠ
생각을 해보니 "리스트 인덱스 범위를 벗어난 경우" 였다. 위의 코드에서 n이 1일 경우에는 리스트 크기가 2이므로, 'answer[2] = 2' 부분에서 에러가 발생한다.
def solution(n):
answer = [0] * (n+1)
answer[1] = 1
if n > 1:
answer[2] = 2
for i in range(3, n+1):
answer[i] = (answer[i-1] + answer[i-2]) % 1234567
return answer[n]
리스트 인덱스 범위를 벗어나지 않게 코드를 수정한 후에 무사히 통과할 수 있었다!!

[Java]
class Solution {
public long solution(int n) {
long[] answer = new long[n+1];
answer[1] = 1;
if (n >1){
answer[2] = 2;
}
for(int i = 3; i < n+1; i++) {
answer[i] = (answer[i-1] + answer[i-2]) % 1234567;
}
return answer[n];
}
}
'프로그래머스' 카테고리의 다른 글
| [프로그래머스] Lv.0 원하는 문자열 찾기 (Python / Java) (0) | 2023.06.27 |
|---|---|
| [프로그래머스] Lv.2 괄호 회전하기 (Python / Java) (0) | 2023.06.23 |
| [프로그래머스] Lv.2 N개의 최소공배수 (Python / Java) (0) | 2023.06.22 |
| [프로그래머스] Lv.2 예상 대진표 (Python / Java) (0) | 2023.06.21 |
| [프로그래머스] Lv.2 Summer/Winter Coding(~2018) 점프와 순간 이동 (Python / Java) (0) | 2023.06.21 |




